 revious post over recursion and stack usage. If you don't remember the initial problem here it is again:
revious post over recursion and stack usage. If you don't remember the initial problem here it is again:"Imagine a robot(say Asimo) that climbs up stairs and has one very simple function step() which succeeds with a probability p and climbs up one stair, and fails with a probability q and climbs down one stair, with p>q and p+q=1. Write a function step_up() guaranteeing that the robot will climb up exactly one stair."
It is easy to create a quick and dirty recursive solution:
void step_up() {
if(!step())
{
step_up();
step_up();
}
}
While this solution is not the best (a better one is provided also in the previous post with the while version), it is most interesting to calculate the number of times that step_up() will be called, in other words to calculate how large the stack size will be.
There were two solutions available: To calculate it analytically or use a recursive technique to do it. With the recursive technique we can set: If X is the number of average calls to step_up() then X = p.1+q.(1+2.X) which yields X = 1 / (p-q) . Both easy and really smart!
However, going analytically is much more difficult but it is most amusing! As I said in the previous post, going the analytical way would mean trouble. Trying it myself I left it unfinished when facing a difficult combinatorics sub-problem. By a really weird coincidence, today I stumbled upon a number of interesting combinatorics tools which could help solve it analytically once and for all!. Here is how it goes.

First, it is clear that is impossible that the step_up() function will be executed an even number of times, for each failed execution two more executions occur. We should wonder: What is the probability that the function will enter 1 time? Clearly it is p. What is the probability of entering 3 times? This would mean failing the first time and succeeding the other 2 times, a total probability of q.p.p = q.p^2. If we want to calculate how many times the function will be executed 5 times we will have to count all possible 'combinations'. We will follow the encoding X1-X2-X3-...-Xn , if we would like to denote a case where the function is executed n times where Xi is either F or S, meaning failure or success at step i respectively.
With this notation we have:
step_up() enters 1 time: Cases: S Combinations:1
step_up() enters 3 times: Cases: F-S-S Combinations:1
step_up() enters 5 times: Cases: F-F-S-S-S, F-S-F-S-S Combinations: 2
step_up() enters 7 times:
Cases: F-F-F-S-S-S-S, F-F-S-F-S-S-S, F-F-S-S-F-S-S, F-S-F-F-S-S-S, F-S-F-S-F-S-S
Combinations: 5
Stop here. There is one important property of every X-X-X-X.. string with n elements, which is that for any initial substring the number of S's is not greater than of the F's. Why? Because if this was the case , the robot would climb up one stair sooner than n steps! Cool! Now, one more thing: It is easy to establish that the last element of the every string will be S, which actually means that the last step of the robot will be to the upwards direction. Ok, this is clear. So let's formulate again the problem.
We have a string with two possible letters, F and S, of length 2.n, in which we have n F's and n S's and for every initial substring the number of S's does not exceed the number of F's. Now we want to calculate the number of all valid combinations for this case. But how to do that? Well, here comes the so-called Dyck words because what we described previously is what exactly how a Dyck word is defined! Now, there is this theorem that states that there exactly Cn Dyck words of length 2.n. What is Cn? But the Catalan numbers of course!
What are the Catalan numbers?? There are defined with the following equation
- and they occur very often in combinatorics problems. In our problem they calculate all possible 'configurations' in which the step_up() function will be called exactly (2.n+1) times (Remember that the last step is always up, this means the last call is always successful). This means that the average calls of step_up() is calculated by,
Now the generating function of the Catalan numbers in the following equation
-

- is given by the equation
-
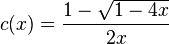
- Using these equations in combination with the derivative of c(x) for the case with the n coefficient it is easy to arrive to to X = 1 / (p-q)
